푸리에 변환(Fourier Transform)은 소음 진동의 분석 뿐만 아니라 오디오 엔지니어링, 이미지 처리를 포함한 많은 분야에서의 중요한 수학적 도구 입니다.
그럼 푸리에 변환이 중요한 이유는 무엇일까요?
푸리에 변환은 타임 도메인 신호를 주파수 도메인으로 변환하는데 사용되며 이것은 종종 신호를 이해하는데 큰 도움이 됩니다.
이것은 마치 아래 그림과 같이 프리즘이 빛을 파장별로 분해하여 보여주듯이 시간신호를 주파수 별로 분해하여 보여주는것과 같은 개념이라고 이해하면 편리할 것 입니다.



모든 신호는 무한개의 Sin 또는 Cos (주기함수)의 합으로 나타낼 수 있다

오늘날 컴퓨터 기반 응용 프로그램에는 이산 푸리에 변환(DFT)와 고속 푸리에 변환(FFT)의 두 가지 종류가 일반적으로 사용 됩니다.
이산 푸리에 변환(DFT)은 연산량이 많아서 컴퓨터로 계산할때 시간이 오래걸리는 단점이 있어서 오늘날에는 이산 푸리에 변환(DFT)을 컴퓨터로 빠르게 계산하기 위한 알고리즘인 고속 푸리에 변환(FFT=Fast Fourier Transform)을 사용 합니다.
즉, 고속 퓨리에 변환(Fast Fourier Transform, FFT)는 아주 적은 계산량으로 DFT를 하는 알고리즘을 의미 합니다.
스펙트럼의 계산 결과는 이산 푸리에 변환(DFT)과 고속 푸리에 변환(FFT)가 100% 동일 하며 고속 푸리에 변환(FFT)의 계산 시간이 훨씬 짧게 걸리기 때문에 측정 장비에는 고속 푸리에 변환(FFT)를 주로 사용 합니다.


위에 그림에 보면 같은 데이터 수 즉, N=1024인 경우 DFT가 약 200배 연산량이 많은 것을 볼 수 있습니다.
참고로 N값이 클수록 아래 그림과 같이 정밀한 스펙트럼을 관찰할 수 있습니다.

N값의 경우 2의 거듭제곱에 해당되는 수를 선택하게끔 되어 있는데 이는 FFT알고리즘이 2의 거듭제곱일 때 더욱 효율적으로 계산하도록 되어 있기 때문 입니다.
주파수 해상도
: 스펙트럼에서 실제 주파수 사이의 간격, 해상도 보다 작은 스펙트럼 변화는 관찰 할 수 없습니다.

예를 들어 샘플링 주파수가 2000Hz인 신호를 N=256 으로 FFT 분석을 하였다면 주파수 해상도는 아래와 같습니다.
2000/2.56=7.8Hz 이 경우 7.8Hz 이하의 스펙트럼 변화는 관찰할 수 없습니다.
주파수 분석시 퓨리에 변환(Fourier Transform)을 수행할때에는 다음과 같이 다양한 스펙트럼 함수가 있습니다.



스펙트럼(Complex Spectrum):
Sx(f): Linear Spectrum으로 불리기도 하며 이것은 x(t) 의 퓨리에 변환으로 부터 유도됩니다.
이것은 실수부(Real)와 허수부(Imaginary)로 구성되어 선택적으로 진폭(Magnitude)과 위상(Phase)으로 표시될 수 있습니다.
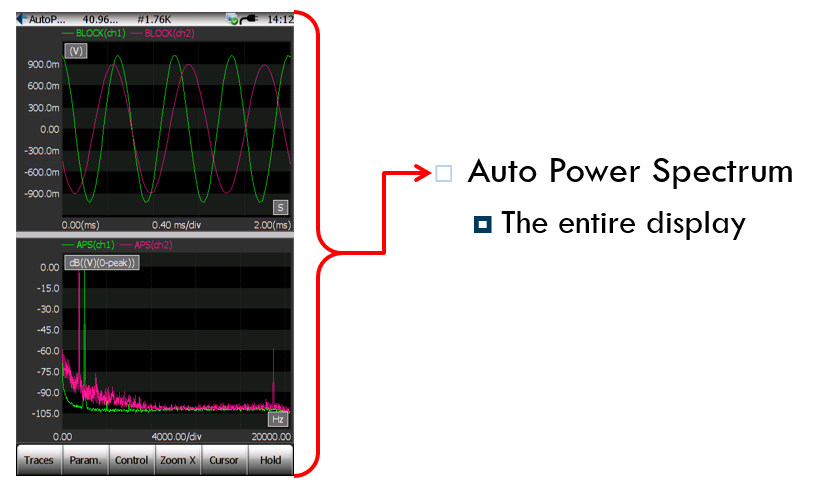
파워 스펙트럼, 오토 파워 스펙트럼(Auto Power Spectrum)은 종종 오토스펙트럼이라고도 합니다.
Gxx는 오토파워 스펙트럼이며 Sx는 주파수 스펙트럼 입니다. Sx*는 주파수 스펙트럼의 공액 복소수 입니다.
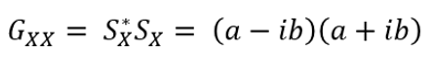
오토파워 스펙트럼은 주파수 스펙트럼에 공액 복소수를 곱한 값 이며 주파수 스펙트럼의 제곱근의 값과 동일하며 실수부(Ral) 값이며 허수부(Imaginary) 정보는 없습니다.
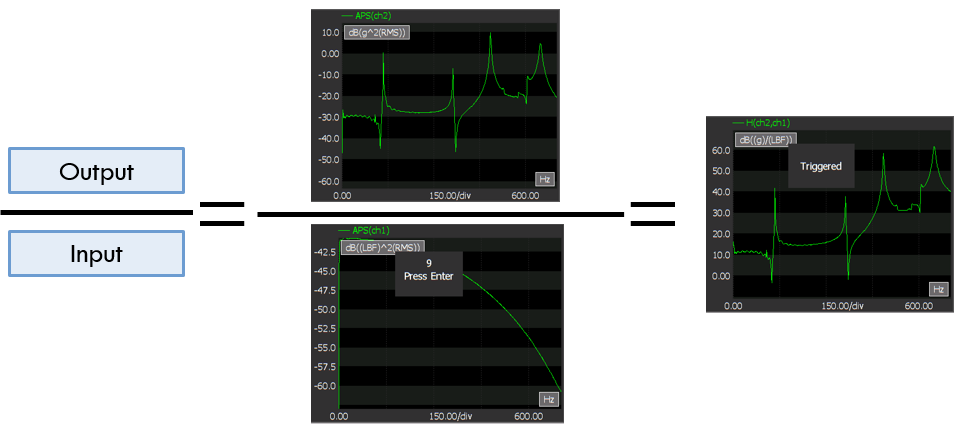
주파수 응답 함수(Frequency Response Function)
FRF Sy/x(f) : Frequency Response function의 줄임말 또는 Transfer function 또는 Response Spectrum Sy(f) 을 input Spectrum Sx(f)으로 나눈 것 입니다. 즉, Sy/x(f) = Sy(f)/ Sx(f) 풀이하면 FRF=응답과 힘의 Cross Spectrum/ 힘의 파워스펙트럼(AutoSpectrum)으로 나눈것과 같다.
FRF 는 complex function으로서 주로 모달 분석 또는 ODS(operational deflection shape)분석에 많이 사용됩니다.
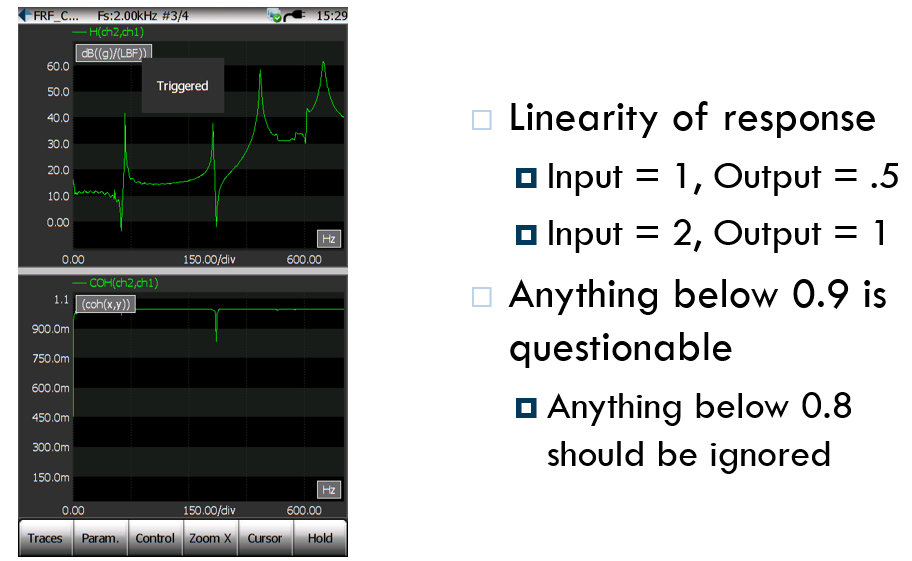
코히런스(Coherence)
두 신호 사이의 선형성 정도를 나타내는 지표로서 각 주파수의 함수로 표현됩니다.
기여도 함수 는 두 신호의 자기 스펙트럼(auto-spectrum)과 상호 스펙트럼(cross-spectrum)으로 다음과 같이 계산됩니다.
Hxy(f) = (|Sxy(f)|)/(|Sx(f)| |Sy(f)|)
기여도 함수값은 0~1의 값을 가지며, 1에 가까울수록 두 신호 사이의 선형 종속 정도가 강하다고 볼 수 있고
그렇지 않다면 값은 0이며 이 코히런스 함수는 보통 모달 시험의 질을 평가하는 보조기능으로 사용됩니다.
크로스 파워 스펙트럼(Cross Power Spectrum)
Cross Spectrum Sxy(f): 이 Cross Spectrum은 Cross Power Spectrum의 줄임말입니다.
Cross Power Spectrum은 Spectrum Sx(f) and Sy(f)의 벡터곱이며 다음과 같이 정의되며
Sxy(f) = Sx(f) Sy*(f), 이것은 복소함수(complex function)이며 종종 벡터장(vector field)에서 사용됩니다.
예를들면 Sound intensity field나 ODS 측정에 주로 사용 됩니다.
파워 스펙트럼 밀도(Power Spectral Density)
대부분의 실제 진동 현상은 정현파가 아닌 랜덤 진동입니다.
FFT는 여러 성분의 정현파 진동 해석에 효과적이긴 하나 랜덤 진동에서는 PSD 분석이 효과적인데
이유는 PSD는 FFT 결과를 복소수 성분과 곱해서 진폭의 실수값 (g^2)을 주파수의 분해능으로 나누어 주기 때문 입니다.
즉 수식으로 표현하자면 g^2/Hz 이 되며 이렇게 되면 주파수 분해능에 대해 비의존적이어서
다른 데이터의 개수를 가지는 신호의 진동 수준을 비교하기에 유용합니다.
상관 분석(Correlation Analysis) 또는 상관관계 분석은 두 신호가 어느 정도 유사한가(유사성)를 정량적으로 분석하는 기법으로 상관계수를 이용하여 측정하는 것입니다. 시간 도메인에서 분석을 하며 레이더 신호의 탐지, 지연 측정 분석에 사용 됩니다.
자기 상관 함수(Auto Correlation Function)
자기 상관 함수는 자기 자신의 신호의 상관계를 측정하는 것으로써 신호가 잡음과 함께 있을 때 그 신호의 주기 검출에 주로 사용 됩니다.
상호 상관 함수(Cross Correlation Function)
상호 상관 함수는 두 신호가 얼마나 유사한가(유사성)를 측정하는 함수 입니다.
특정 패턴의 신호를 찾거나 디지털 이미지 처리등에 사용 됩니다.
'기술자료실' 카테고리의 다른 글
| [공유]NVH(Noise, Vibration, Harshness) 차원이 다르게 소리를 제어하다 (0) | 2022.04.29 |
|---|---|
| Operating Deflection Shape(ODS)을 이용한 진동 분석 (0) | 2022.04.29 |
| 모달 테스트(Modal Test)을 이용한 구조물의 동특성 측정 (0) | 2022.04.27 |
| 회전체 진동 신호 및 분석 기법(Orbit & Shaft Center Line & Bode Plot) (0) | 2022.04.27 |
| 미세 진동의 측정 (0) | 2022.04.25 |




댓글